Until only recently I believed there were Bernoulli trials and a Binomial distribution and a Bernoulli distribution does not exist. It was my understanding that when simulating a standard AB test with a binary outcome (such as a purchase or subscription), each visitor amounts to a Bernoulli trial and the behaviour for multiple Bernoulli trials is described by the Binomial distribution.
It turns out I was completely right other than in my belief that there is no such thing as a Bernoulli distribution.
Note: guy in painting is Jacob Bernoulli (1654-1705) who derived each of the distributions and of course the trials too.
Bernoulli trials
These can be readily defined as a single experiment where the outcome is binary. The probability of a success (or 1) is $p$ and the probability of a failure (or 0) is therefore 1-p. This is much like a website conversion test where we measure whether a visit results in a purchase or not.
Defining this experiment statistically and using terms such as random variables, probability mass functions takes us to the Bernoulli distribution.
Bernoulli distribution
Using mathematical notation, we can define the Bernoulli distribution as the discrete probablility distribution for the random variable \(X\) where the probability function is
\[P(X) = \begin{cases} p&\text{for $x=1$}\\ 1-p&\text{for $x=0$}\\ \end{cases}\]The Bernoulli distribution strictly covers the distribution for a random variable which has a binary outcome for one single Bernoulli trial.
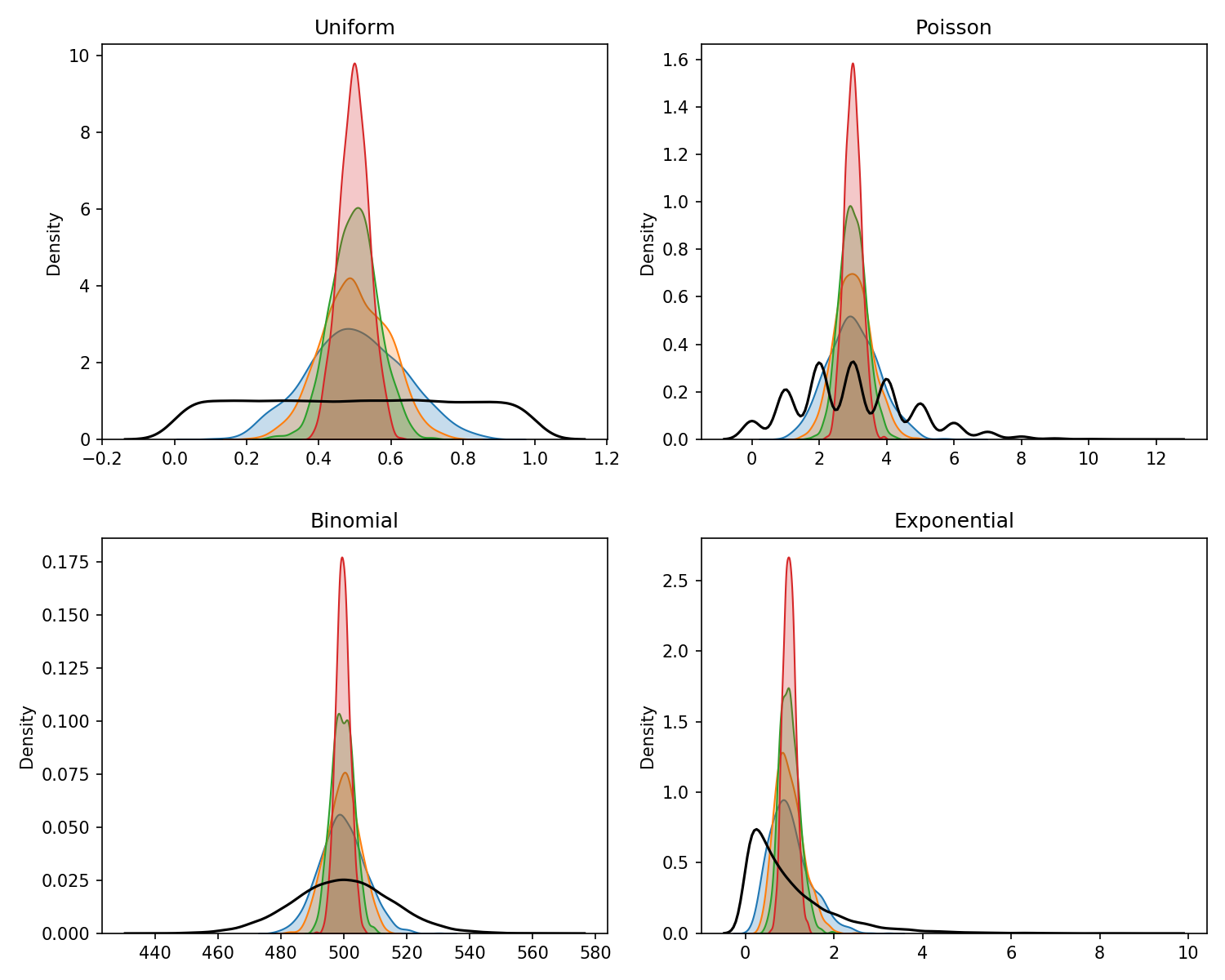
If we want to run more than one trial, which is the case when running AB tests, we need the Binomial distribution to help understand the behaviour of the data.
Binomial distribution
The Binomial Distribution represents the number of successes and failures in n independent Bernoulli trials for some given value of n.
This is the typical definition. It’s clear here that if \(n\) were equal to 1 we would have the Bernoulli distribution showing how the Bernoulli distribution is a form or subset of the Binomial distribution.
Conclusion
I don’t want to dive much further into explaining the Binomial distribution as many other articles will do a better job of it. Here I simply wanted to point out the differences and highlight that there is a Bernoulli distribution, technically.
All random variables in fact do have a distribution by their very nature.
The final thing I would like to say is on why I found this important and why I believe it’s important to know the differences between these distributions and about distributions generally. I’m currently using the Binomial distribution to define the prior distribution for Bayesian AB testing following Cameron Davidson-Pilons book ‘Bayesian Methods for Hackers’.
Identifying which distribution is suitable for a random variable is key to understanding it’s behaviour and knowing which assumptions we can make when doing analysis. The binomial distribution is one of the simpler distributions and any budding statistician is bound to come across it, especially as every book about probability distribution seems contractually obliged to include at least one coin-flip example.